报告一:
报告人:孙琪
单位:北京工商大学
时间:2020年10月7日 周三下午15:00-16:00
线上腾讯会议,会议号:551638602
题目:Lower deviations for supercritical branching processes with immigration
摘要:
For a supercritical branching processes with immigration 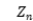 , it is known that under suitable conditions on the offspring and immigration distributions,
, it is known that under suitable conditions on the offspring and immigration distributions, 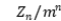 converges almost surely to a finite and strictly positive limit, where
converges almost surely to a finite and strictly positive limit, where 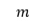 is the offspring mean. We are interested in the limiting properties of
is the offspring mean. We are interested in the limiting properties of 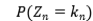 with
with 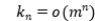 as
as 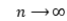 . We give asymptotic behavior of such lower deviation probabilities in both Schr\"{o}der and B\"{o}ttcher cases, unifying and extending the previous results for non-immigration cases in literature.
. We give asymptotic behavior of such lower deviation probabilities in both Schr\"{o}der and B\"{o}ttcher cases, unifying and extending the previous results for non-immigration cases in literature.
This talk is based on joint work with Professor Mei Zhang.
报告二:
报告人:李豆豆
单位:北京工业大学
时间:2020年10月7日 周三下午16:00-17:00
线上腾讯会议,会议号:551638602
题目:Harmonic moments and large deviations for a critical Galton-Watson process with immigration
摘要:
In this paper, a critical Galton-Watson branching process with immigration 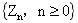 is studied. We first obtain the convergence rate of the harmonic moment of
is studied. We first obtain the convergence rate of the harmonic moment of 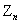 . Then the large deviation of
. Then the large deviation of 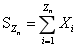 is obtained, where
is obtained, where 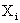 is a sequence of independent and identically distributed zero-mean random variables with tail index α>2. We shall see that the converging rate is determined by the immigration mean, the variance of reproducing and the tail index of
is a sequence of independent and identically distributed zero-mean random variables with tail index α>2. We shall see that the converging rate is determined by the immigration mean, the variance of reproducing and the tail index of 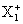 , comparing to previous result for supercritical case, where the rate depends on the Schröder constant and the tail index.
, comparing to previous result for supercritical case, where the rate depends on the Schröder constant and the tail index.
This is a joint work with Professor Mei Zhang.












