2020.12.23 ,贺劲松 教授,The kink solutions of the SIdV equation and the associated surfaces
发布时间: 2020-12-21 10:18 作者: 点击: 373
学术报告
题 目: |
The kink solutions of the SIdV equation and the associated surfaces |
报告人: |
贺劲松 教授,深圳大学高等研究院 |
摘 要: |
In this talk, we study a new non-linear integrable equation, 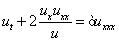
which is invariant under scaling of dependent variable and was called the SIdV equation, see Commun. Nonlinear Sci. Numeric. Simulat. 17 (2012) 4155. The order-n kink solution  of the SIdV equation, which is associated with the n-soliton solution of the Korteweg-de Vries equation, is constructed by using the n-fold Darboux transformation (DT) from zero “seed” solution. Moreover, we also provide the evolution scenarios of surfaces of revolution associated with the kink-type solutions of the SIdV, where the kink-type solutions play the role of a metric. We put forward two kinds of evolution scenarios for surfaces of revolution associated with two types of kink-type metric (solution) and we study the key properties of these surfaces. of the SIdV equation, which is associated with the n-soliton solution of the Korteweg-de Vries equation, is constructed by using the n-fold Darboux transformation (DT) from zero “seed” solution. Moreover, we also provide the evolution scenarios of surfaces of revolution associated with the kink-type solutions of the SIdV, where the kink-type solutions play the role of a metric. We put forward two kinds of evolution scenarios for surfaces of revolution associated with two types of kink-type metric (solution) and we study the key properties of these surfaces. |
时 间: |
12月23日 星期三 9:00—10:30 |
方 式: |
腾讯会议 会议 ID:942 743 554 会议密码:1223 |
邀请人: |
刘青平 教授 |











